The Vector Heat Method

Abstract
This paper describes a method for efficiently computing parallel transport of tangent vectors on curved surfaces, or more generally, any vector-valued data on a curved manifold. More precisely, it extends a vector field defined over any region to the rest of the domain via parallel transport along shortest geodesics. This basic operation enables fast, robust algorithms for extrapolating level set velocities, inverting the exponential map, computing geometric medians and Karcher/Fréchet means of arbitrary distributions, constructing centroidal Voronoi diagrams, and finding consistently ordered landmarks. Rather than evaluate parallel transport by explicitly tracing geodesics, we show that it can be computed via a short-time heat flow involving the connection Laplacian. As a result, transport can be achieved by solving three prefactored linear systems, each akin to a standard Poisson problem. Moreover, to implement the method we need only a discrete connection Laplacian, which we describe for a variety of geometric data structures (point clouds, polygon meshes, etc.). We also study the numerical behavior of our method, showing empirically that it converges under refinement, and augment the construction of intrinsic Delaunay triangulations (iDT) so that they can be used in the context of tangent vector field processing.
Selected figures

We demonstrate the use of heat flow to interpolate scalar or vector data from isolated sources across a curved surface. With a single step of very short time flow, the result provably converges to nearest-neighbor interpolation.

Results of the vector heat method on a variety of models; a source vector marked by a large arrow is extended across a surface via parallel transport along shortest geodesics.

To implement our method on a given geometric data structure, we essentially just need a scalar Laplacian and a notion of tangent spaces at each point or vertex. Here we show the solution for three sources of different magnitudes on a triangle mesh, point cloud, polygon mesh, and voxelization.
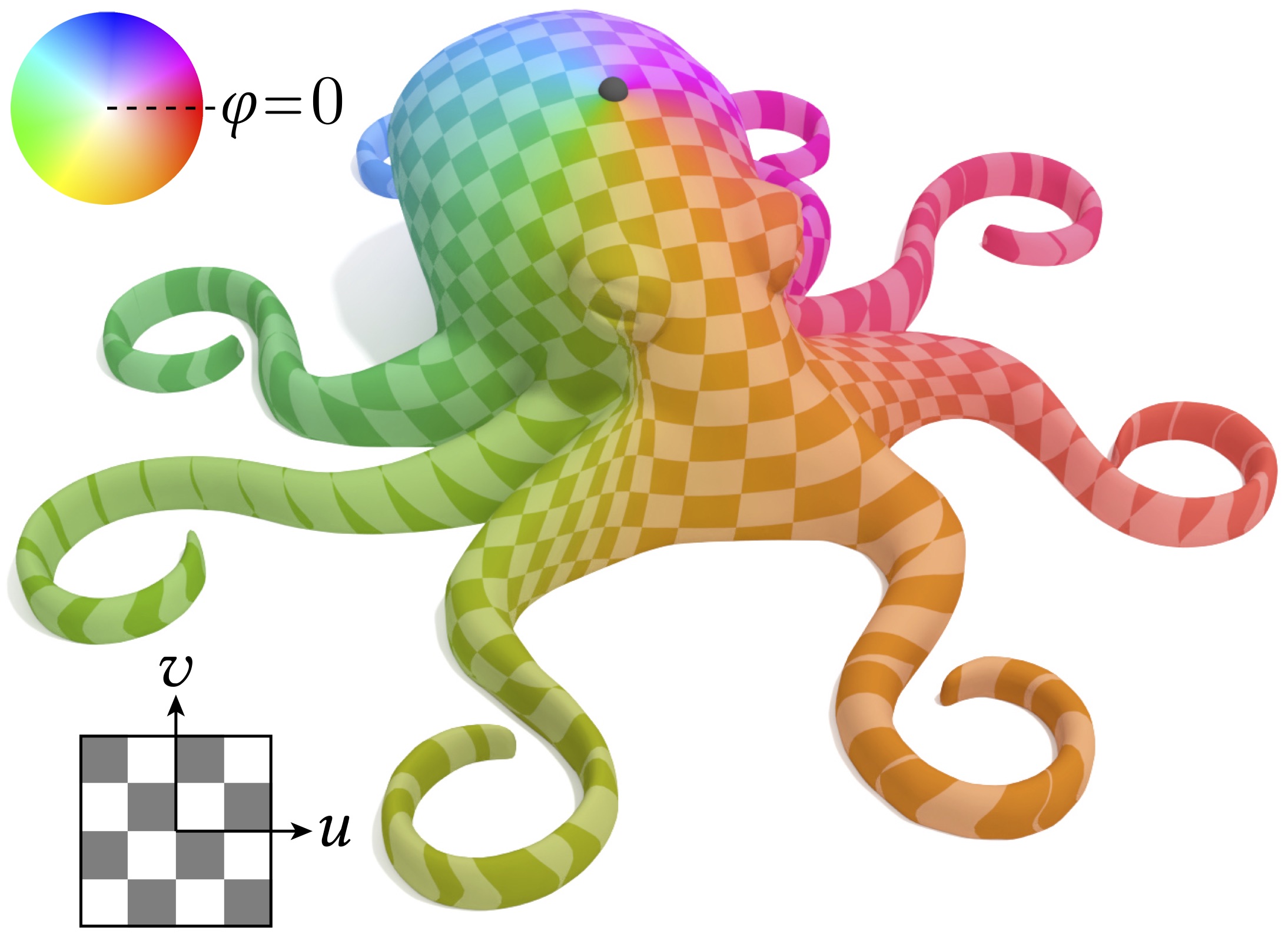
The vector heat method provides the missing numerical ingredient to compute the logarithmic map: a parameterization about a source point which encodes the length and direction of shortest paths emanating from that point.
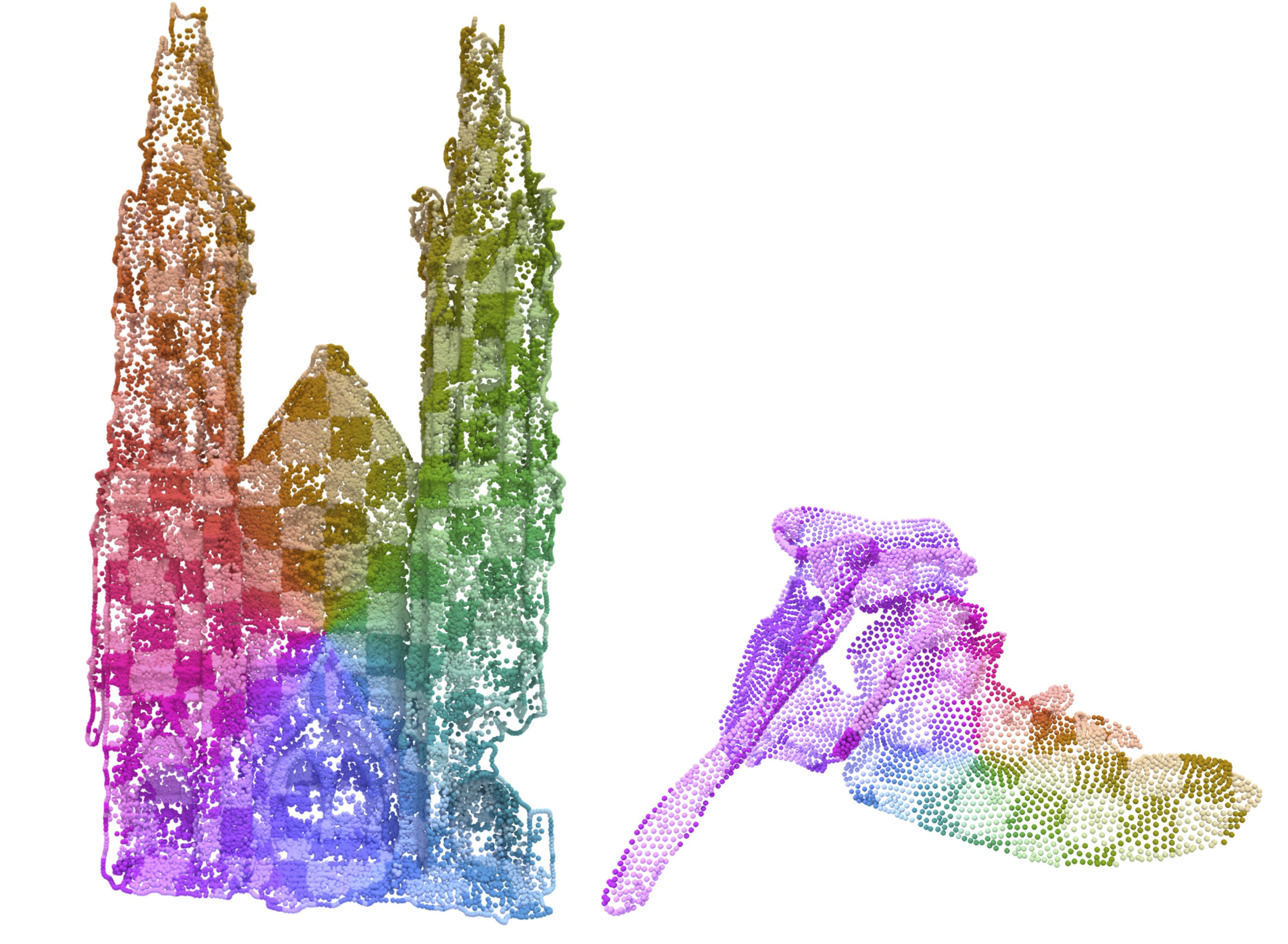
Since the vector heat method is easily applied to various discretizations, we can also compute a logarithmic map on a point cloud.
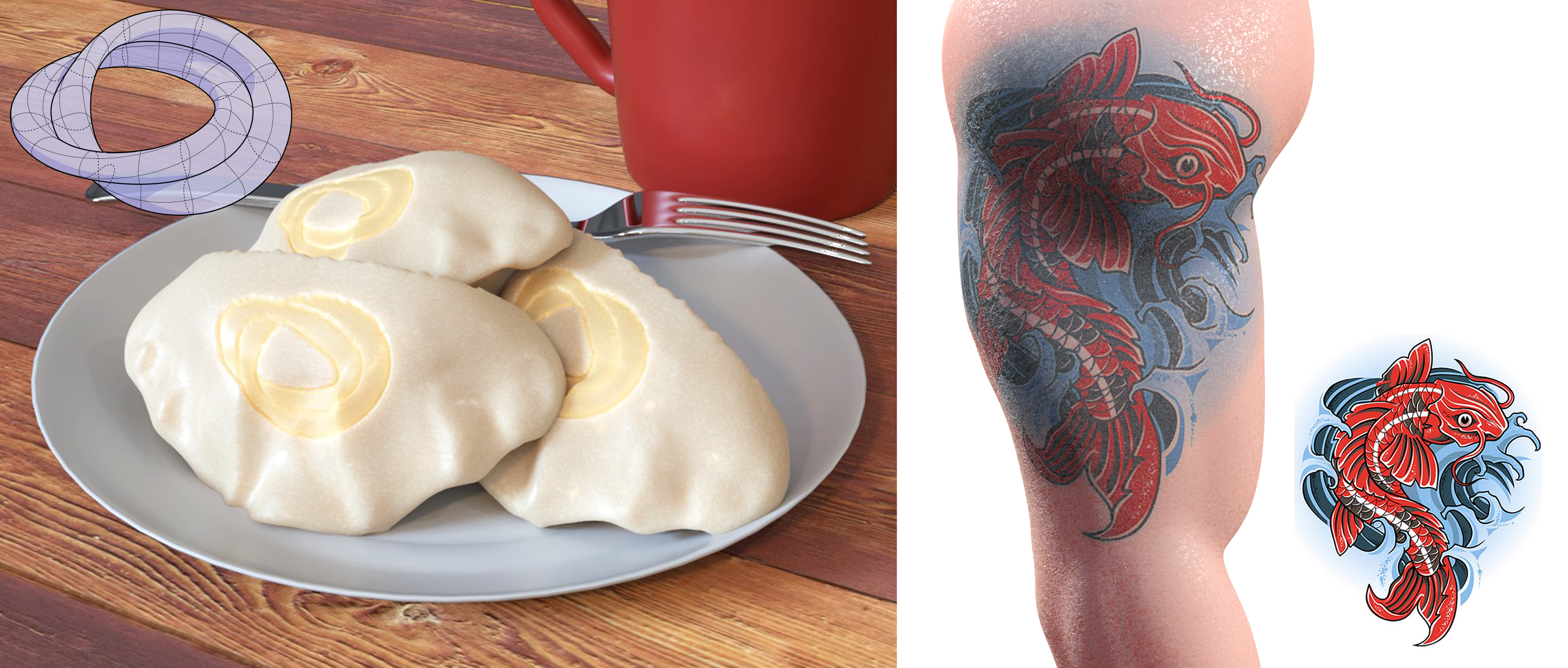
A noise-free log map allows us to place delicious decals or tantalizing tattoos on a surface without having to worry about difficult issues like where to place cuts.
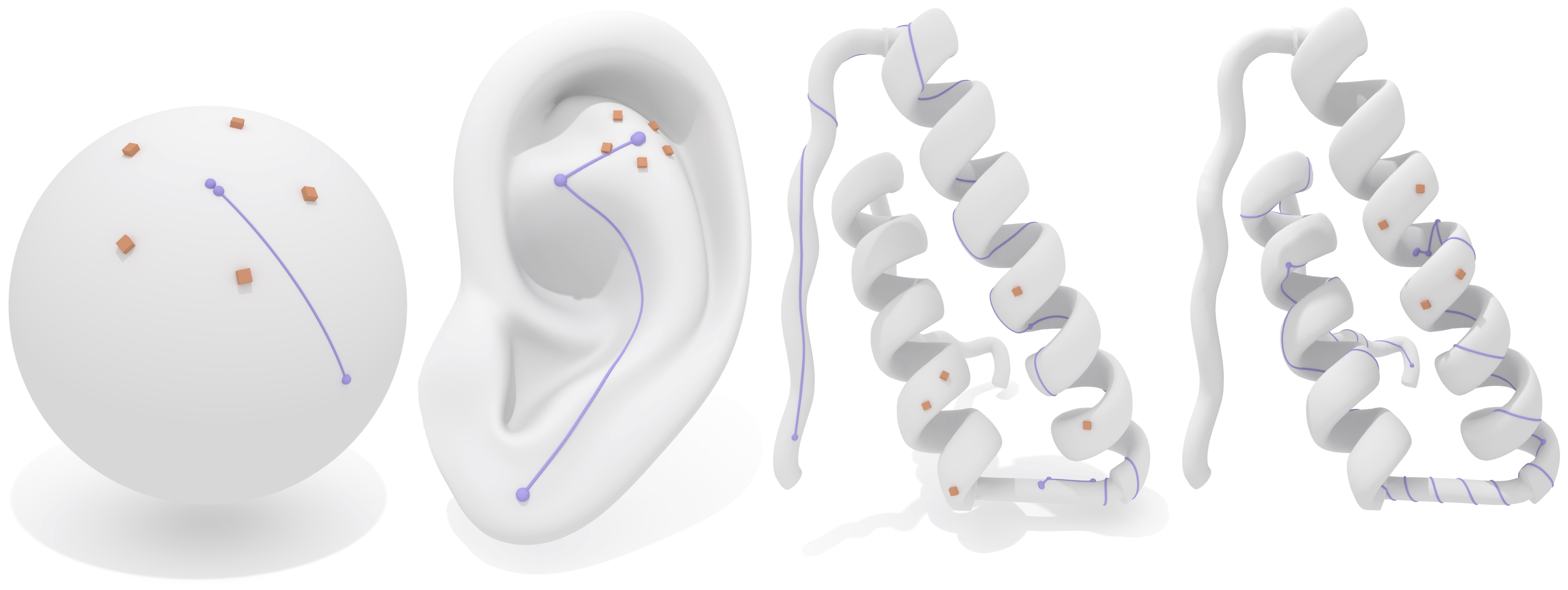
Our globally accurate logarithmic map can be used to compute centers of of point sets or distributions on curved surfaces (called Karcher/Fréchet means).
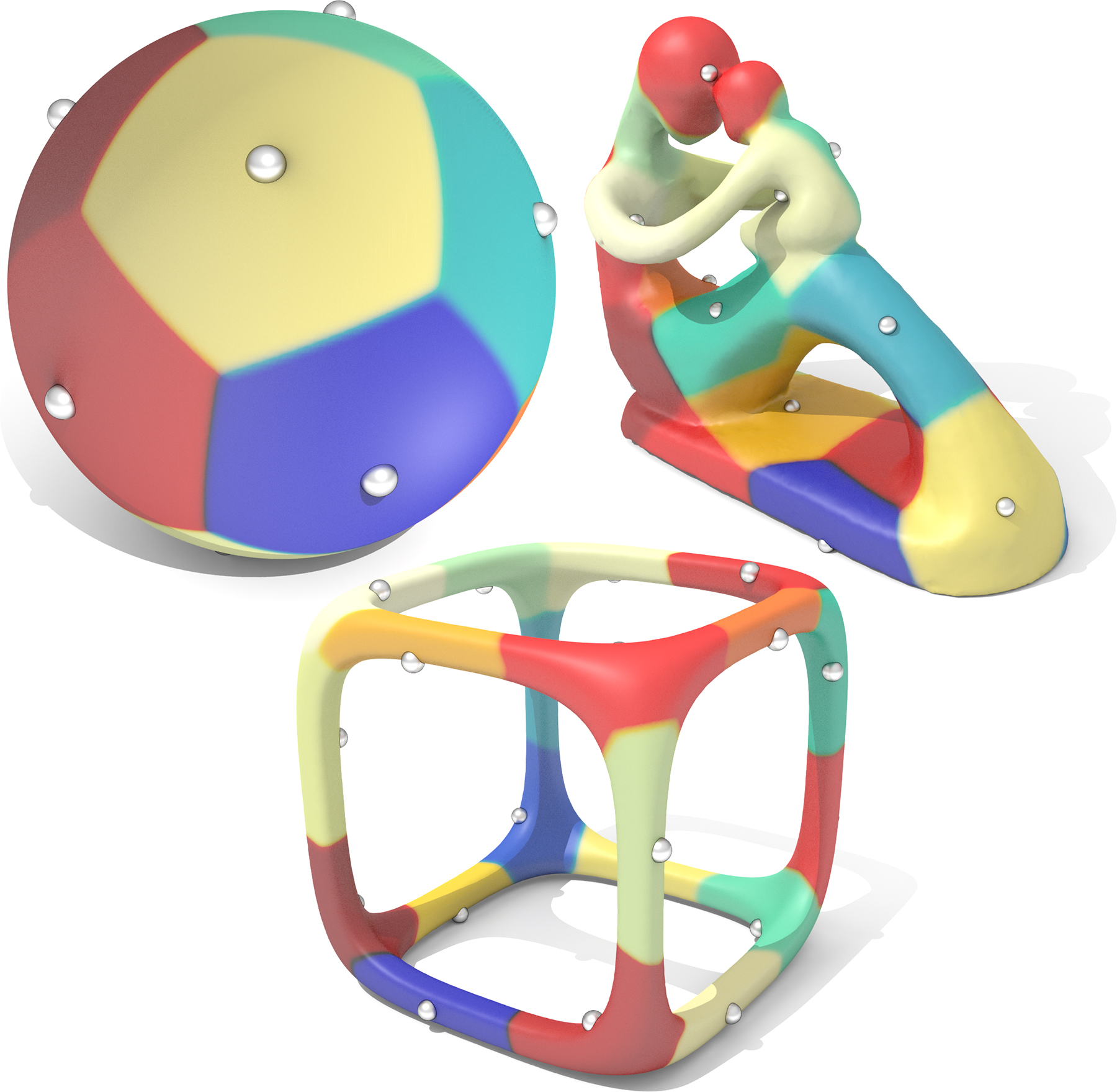
Fast Karcher means allow us to compute centroidal geodesic Voronoi tesselations with large, possibly multiply connected cells.