Spelunking the Deep: Guaranteed Queries on General Neural Implicit Surfaces via Range Analysis
Best Paper Award
Abstract
Neural implicit representations, which encode a surface as the level set of a neural network applied to spatial coordinates, have proven to be remarkably effective for optimizing, compressing, and generating 3D geometry. Although these representations are easy to fit, it is not clear how to best evaluate geometric queries on the shape, such as intersecting against a ray or finding a closest point. The predominant approach is to encourage the network to have a signed distance property. However, this property typically holds only approximately, leading to robustness issues, and holds only at the conclusion of training, inhibiting the use of queries in loss functions. Instead, this work presents a new approach to perform queries directly on general neural implicit functions for a wide range of existing architectures. Our key tool is the application of range analysis to neural networks, using automatic arithmetic rules to bound the output of a network over a region; we conduct a study of range analysis on neural networks, and identify variants of affine arithmetic which are highly effective. We use the resulting bounds to develop geometric queries including ray casting, intersection testing, constructing spatial hierarchies, fast mesh extraction, closest-point evaluation, evaluating bulk properties, and more. Our queries can be efficiently evaluated on GPUs, and offer concrete accuracy guarantees even on randomly-initialized networks, enabling their use in training objectives and beyond. We also show a preliminary application to inverse rendering.
Selected figures
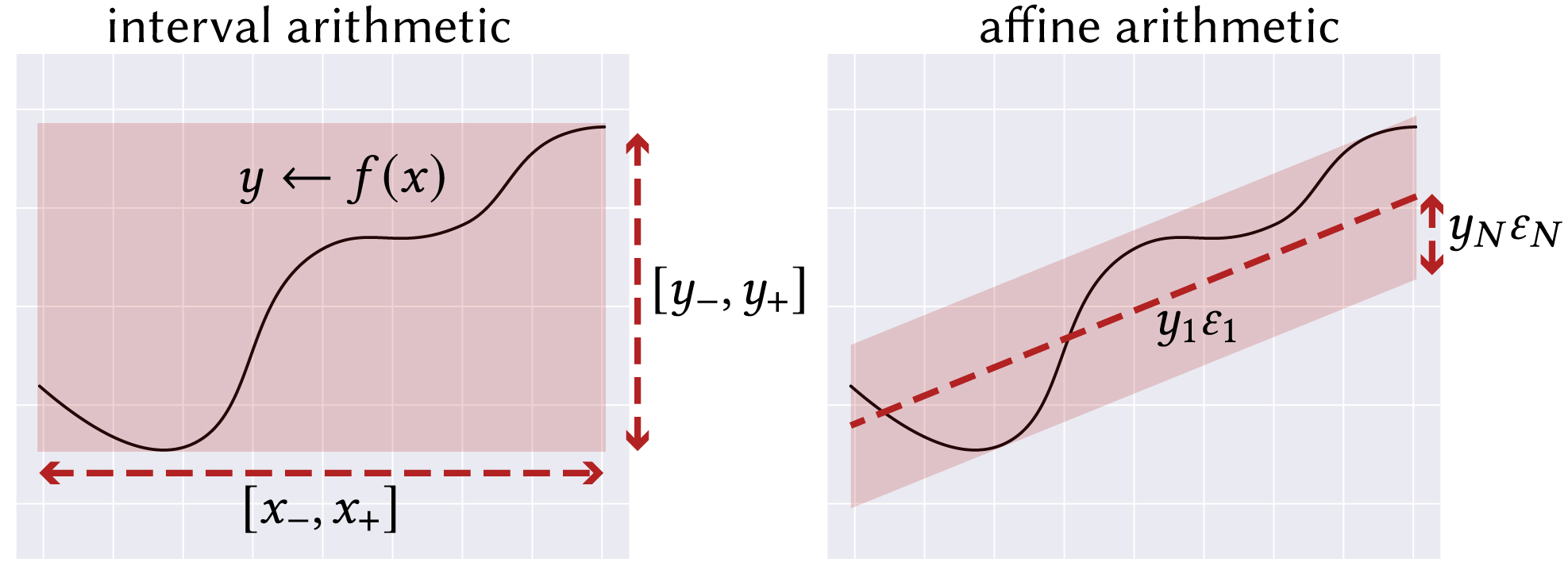
Queries are performed by applying affine arithmetic, a kind of range analysis, to neural networks. Affine arithmetic models the correlation between quantities to achieve much tighter bounds than simple interval arithmetic.
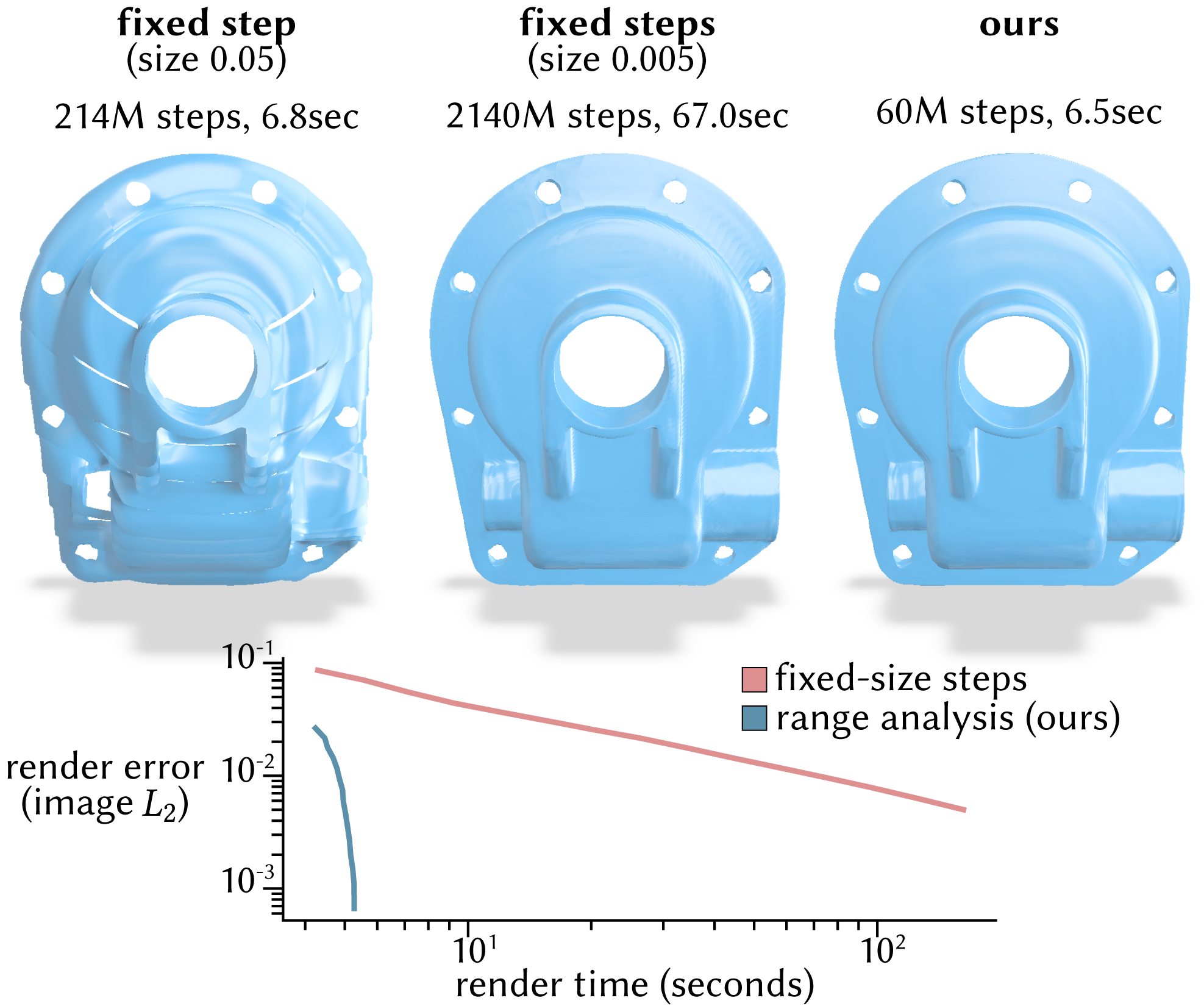
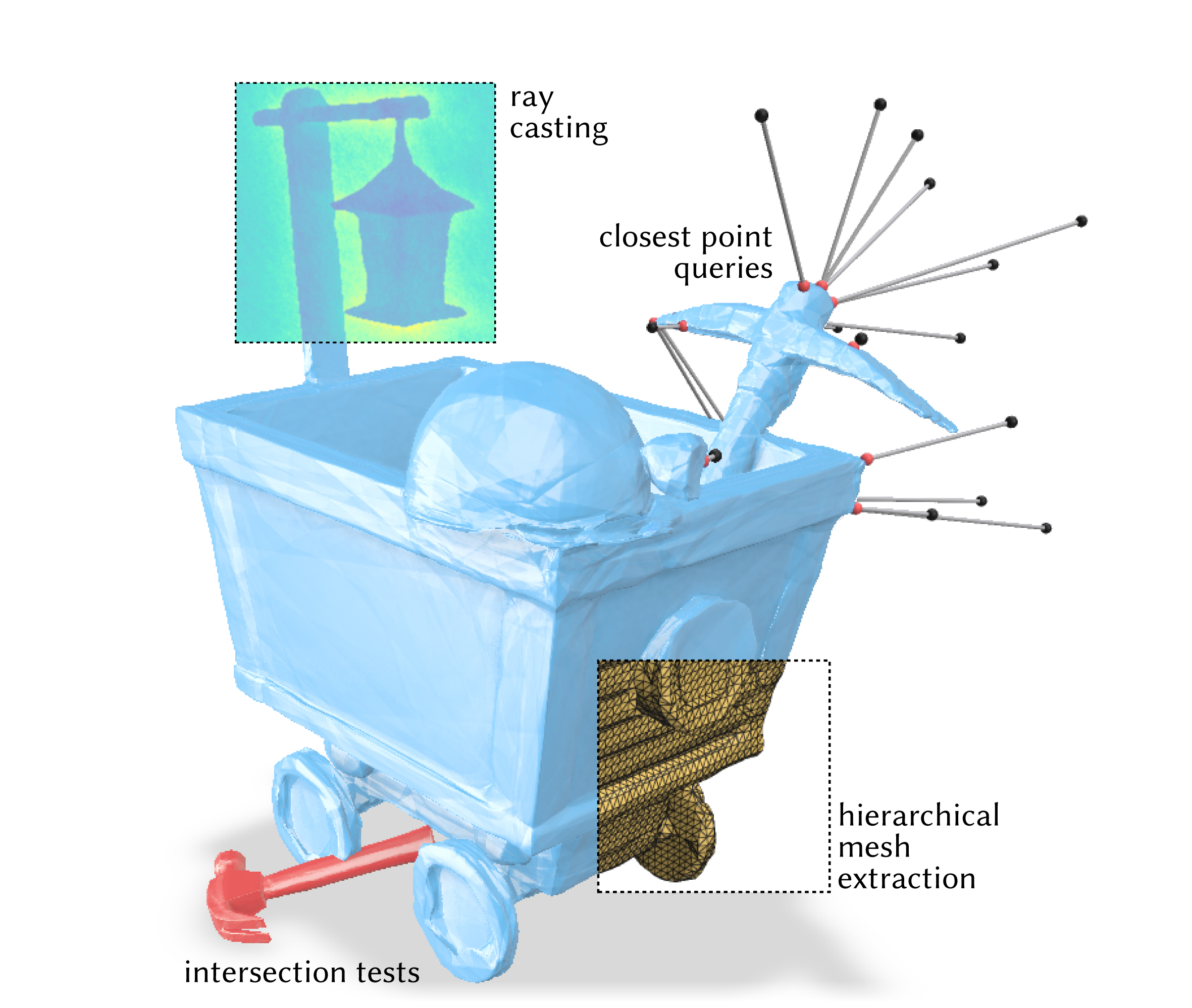
Previously, casting rays against general neural implicit surfaces required small, fixed-sized steps, used here to render an image. Large steps can miss parts of the surface (top, left), but smaller steps are expensive (top, middle). Our approach avoids tuning a step size, and is much faster. (top, right). We measure this effect via the image error at various render time budgets (bottom), varying the fixed step size or our convergence parameter 𝛿, respectively.
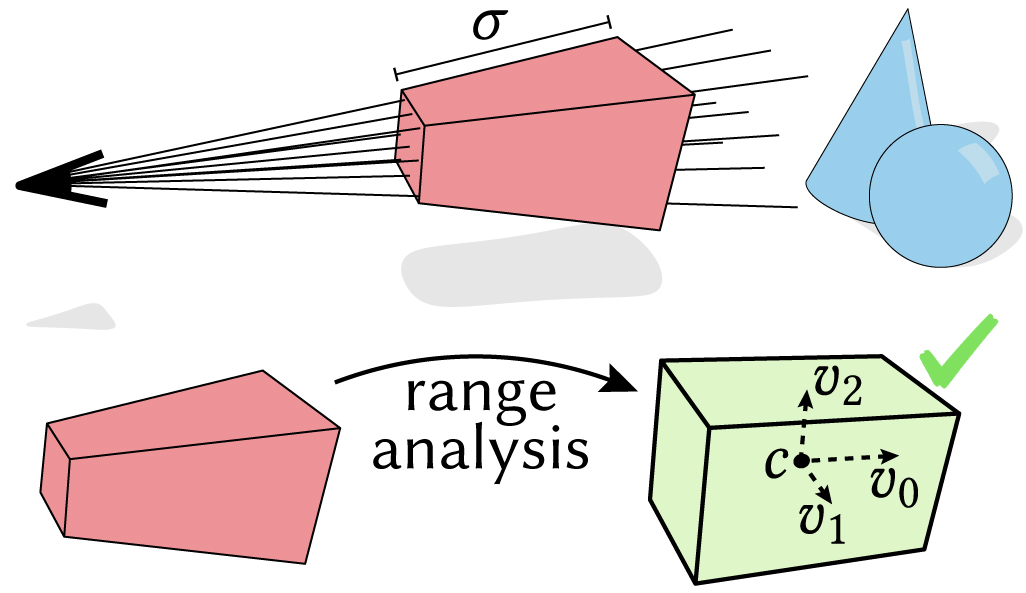
Range analysis also enables an image-space acceleration of ray casting by testing whole frustums of rays simultaneously, saving repeated similar computation.
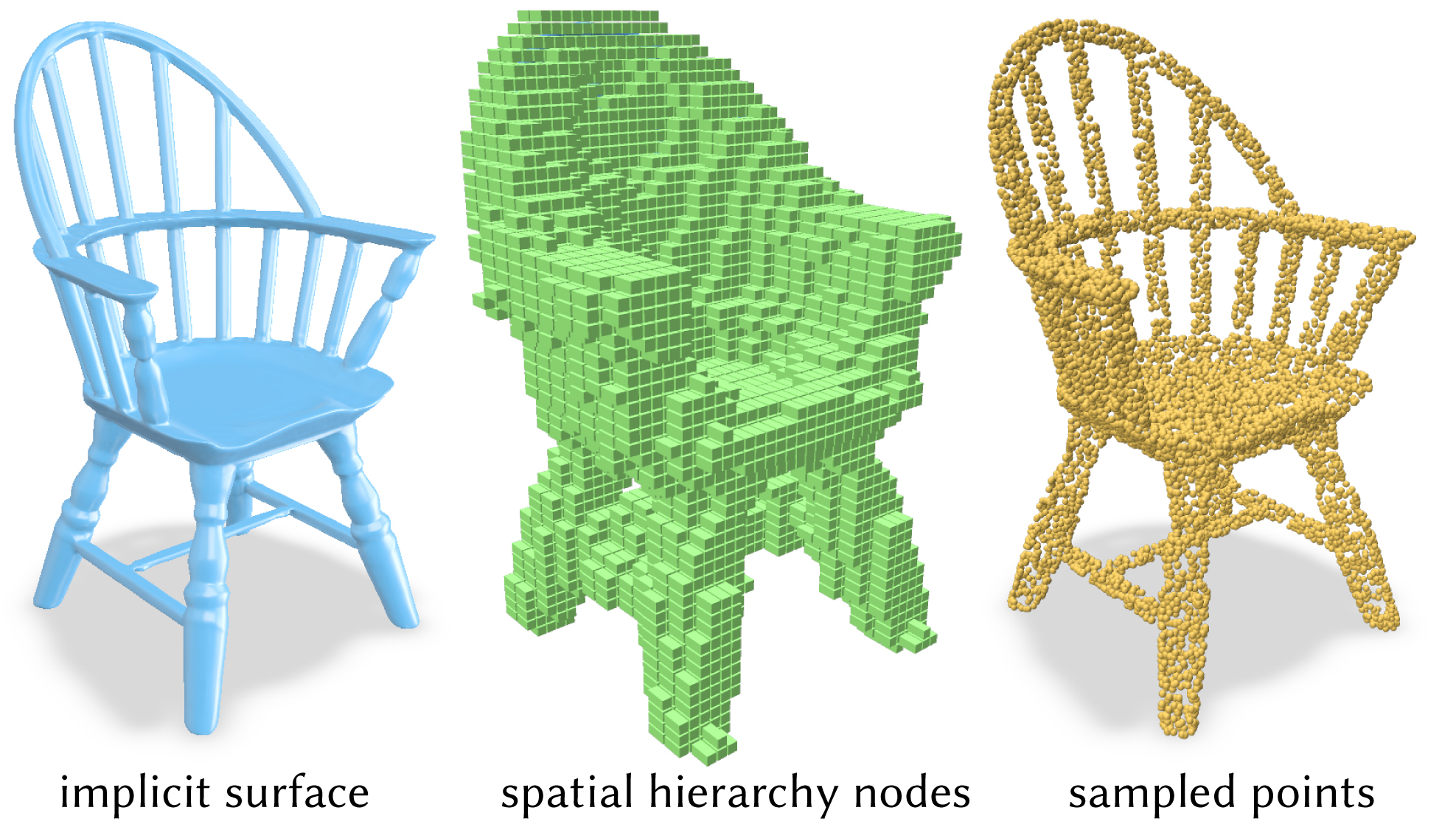
Range analysis can also be used to build spatial acceleration structures like k-D trees over neural implicit surfaces. Sampling a points on a surface is a common task in geometric learning—these spatial hierarchies can be used to sample efficiently, outperforming naive rejection sampling by an order of magnitude for large sample sets.
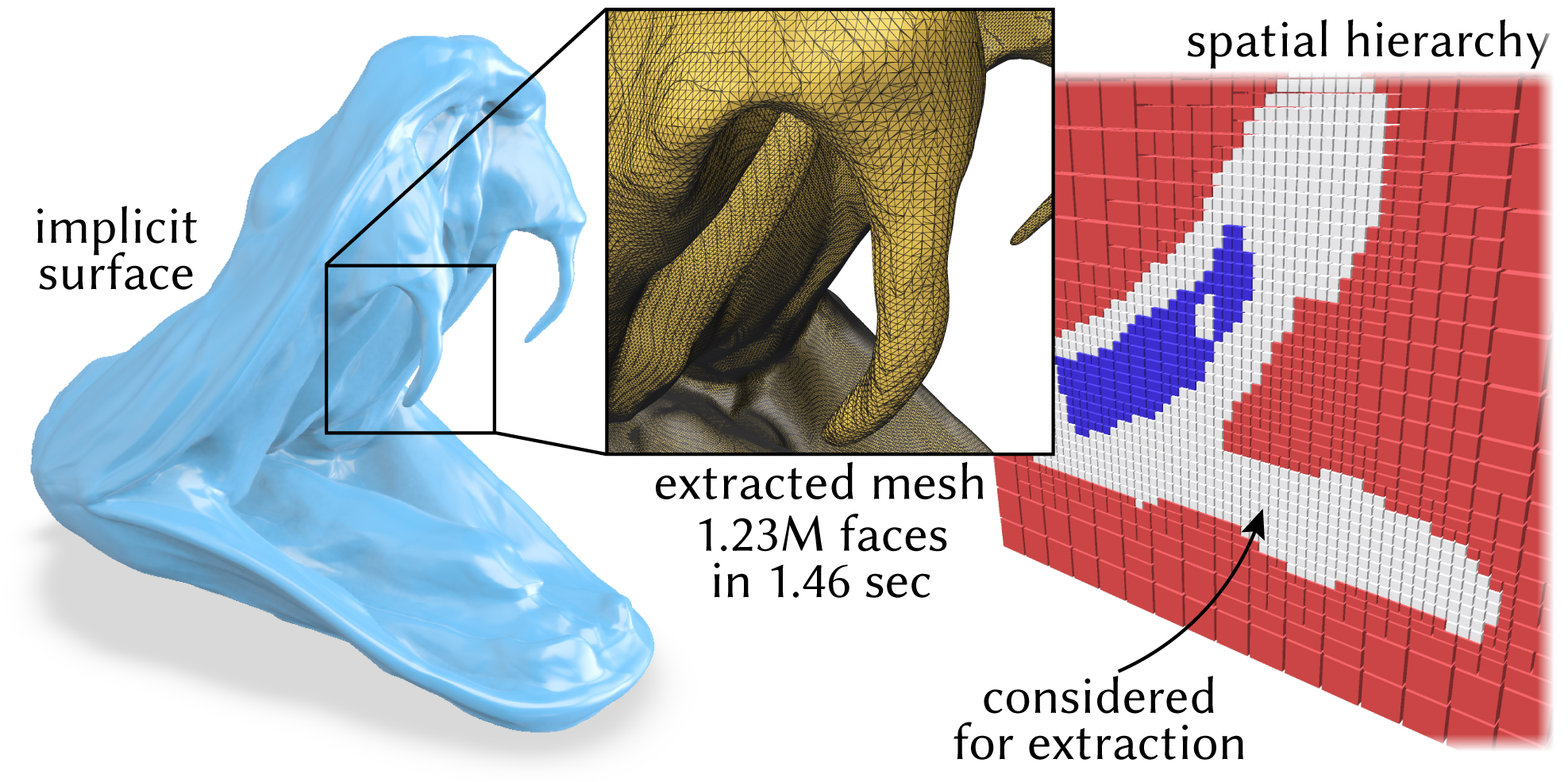
If an explicit mesh is desired, our spatial bounding hierarchy enables an adaptive variant of marching cubes which avoids evaluating the function in large empty regions. This yields the same output as ordinary dense marching cubes, but scales much more efficiently to high-resolution meshes.
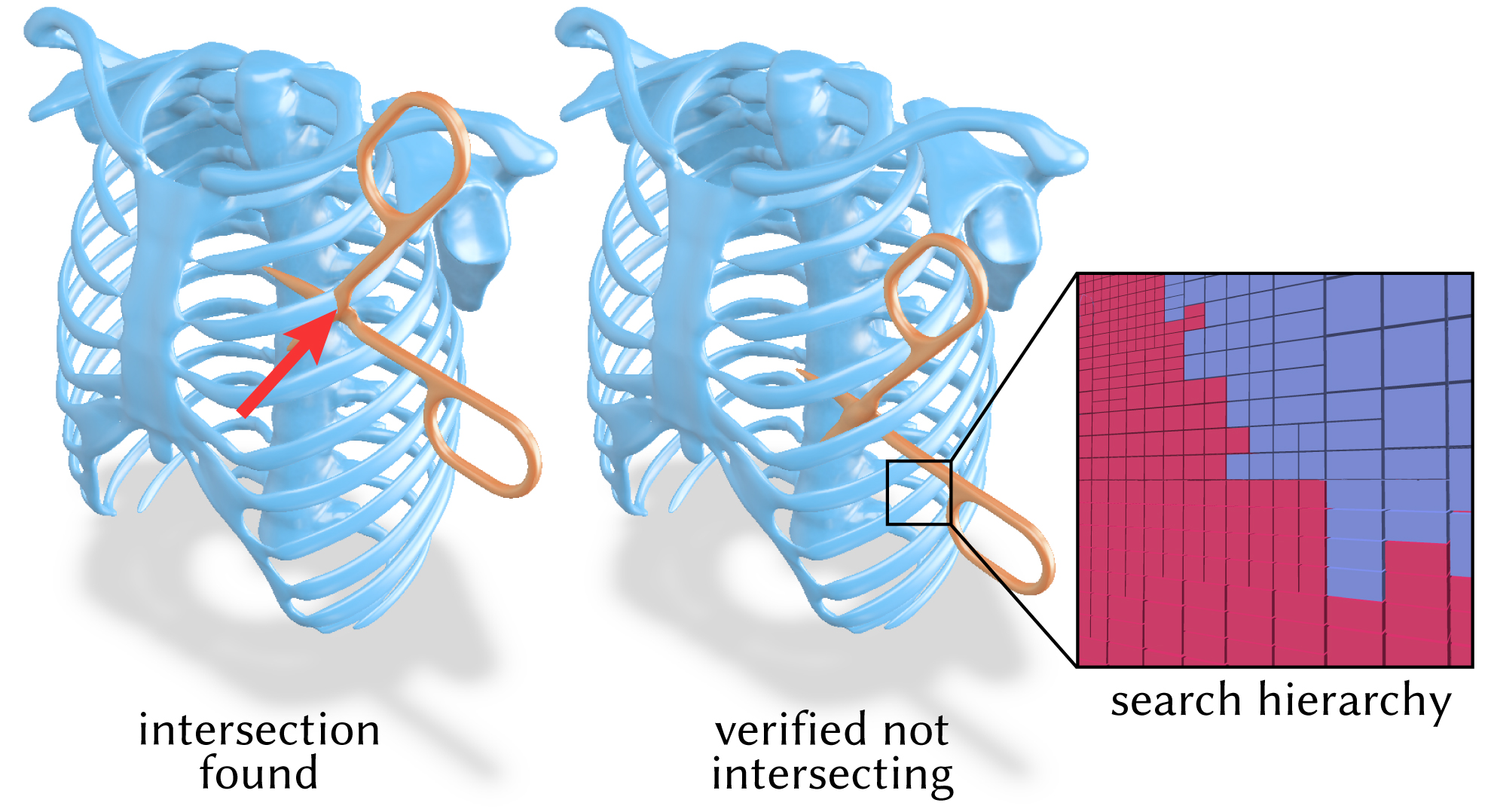
Our queries are used to detect intersections between a pair of general neural implicit shapes. The inset image shows the k-d tree used to bound the space. Each cell has been verified to not overlap with at least one of the two shapes, indicated by the color.
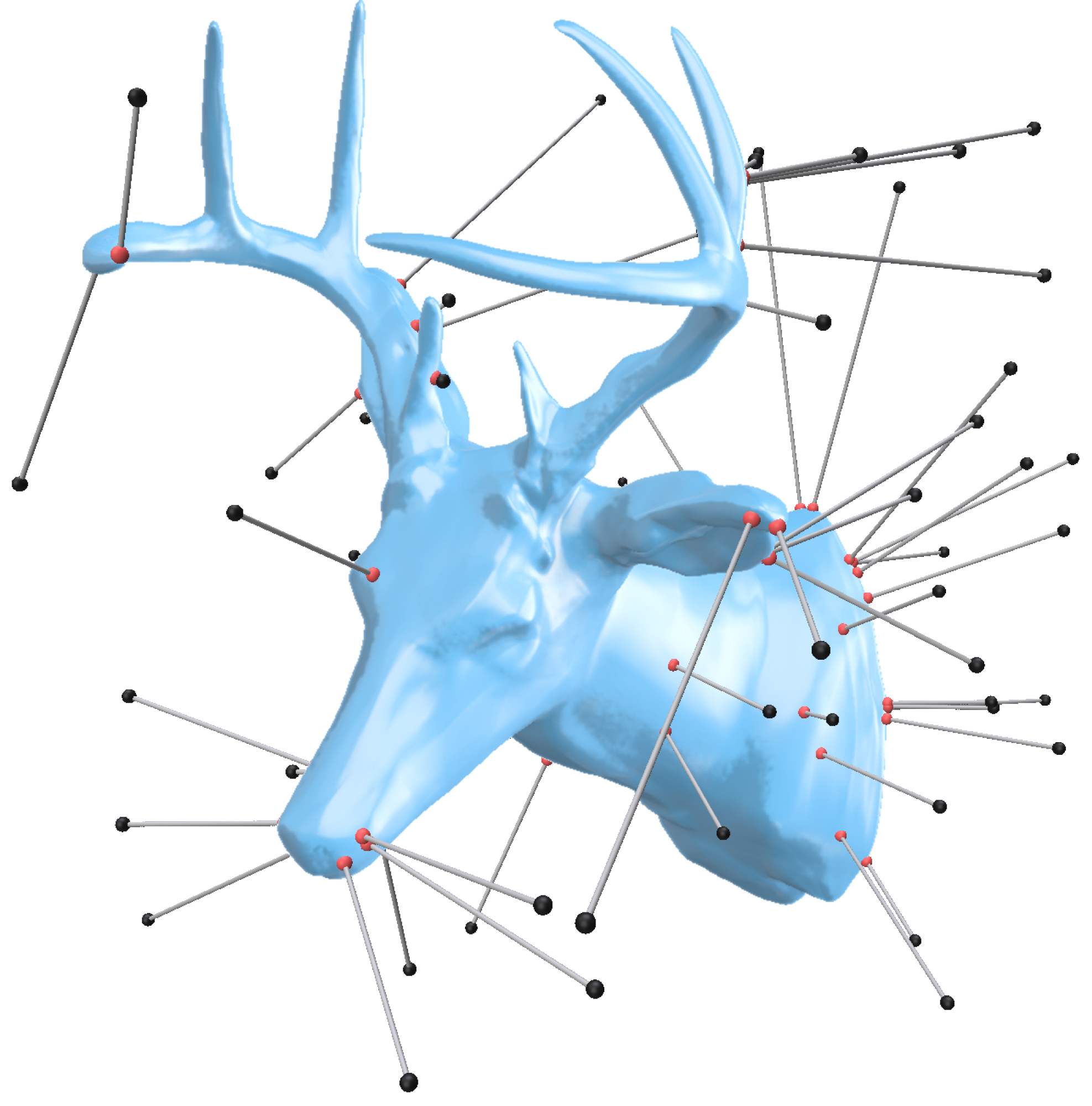
Our method projects query points to the closest point on the neural implicit level set. Black query points are sampled randomly in space, red points are their projections.