PointTriNet: Learned Triangulation of 3D Point Sets
Abstract
This work considers a new task in geometric deep learning: generating a triangulation among a set of points in 3D space. We present PointTriNet, a differentiable and scalable approach enabling point set triangulation as a layer in 3D learning pipelines. The method iteratively applies two neural networks: a classification network predicts whether a candidate triangle should appear in the triangulation, while a proposal network suggests additional candidates. Both networks are structured as PointNets over nearby points and triangles, using a novel triangle-relative input encoding. Since these learning problems operate on local geometric data, our method is efficient and scalable, and generalizes to unseen shape categories. Our networks are trained in an unsupervised manner from a collection of shapes represented as point clouds. We demonstrate the effectiveness of this approach for classical meshing tasks, robustness to outliers, and as a component in end-to-end learning systems.
Selected figures

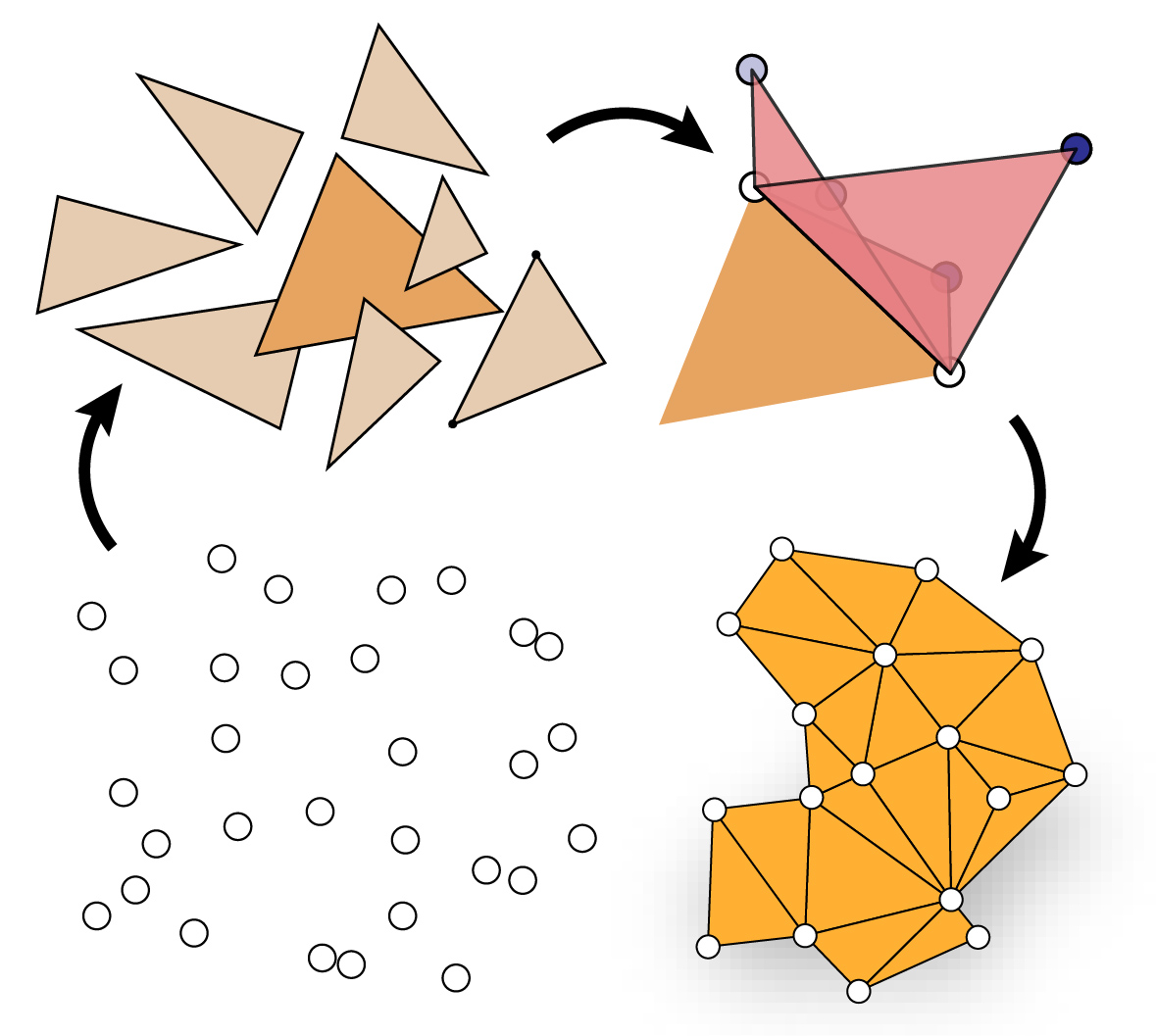
An overview of our PointTriNet pipeline, which generates a triangulation by alternating between proposing new triangles and classifying them, each with a neural network. The classifier network identifies triangles which should appear in the triangulation, while the proposal network generates new candidates.

The core of our technique is a network which classifies whether a given triangle belongs in a triangulation, as a function of nearby points and already-classified candidates. All coordinates are encoded relative to the query triangle. A second, similarly-structured network proposes new triangle candidates for subsequent classification.
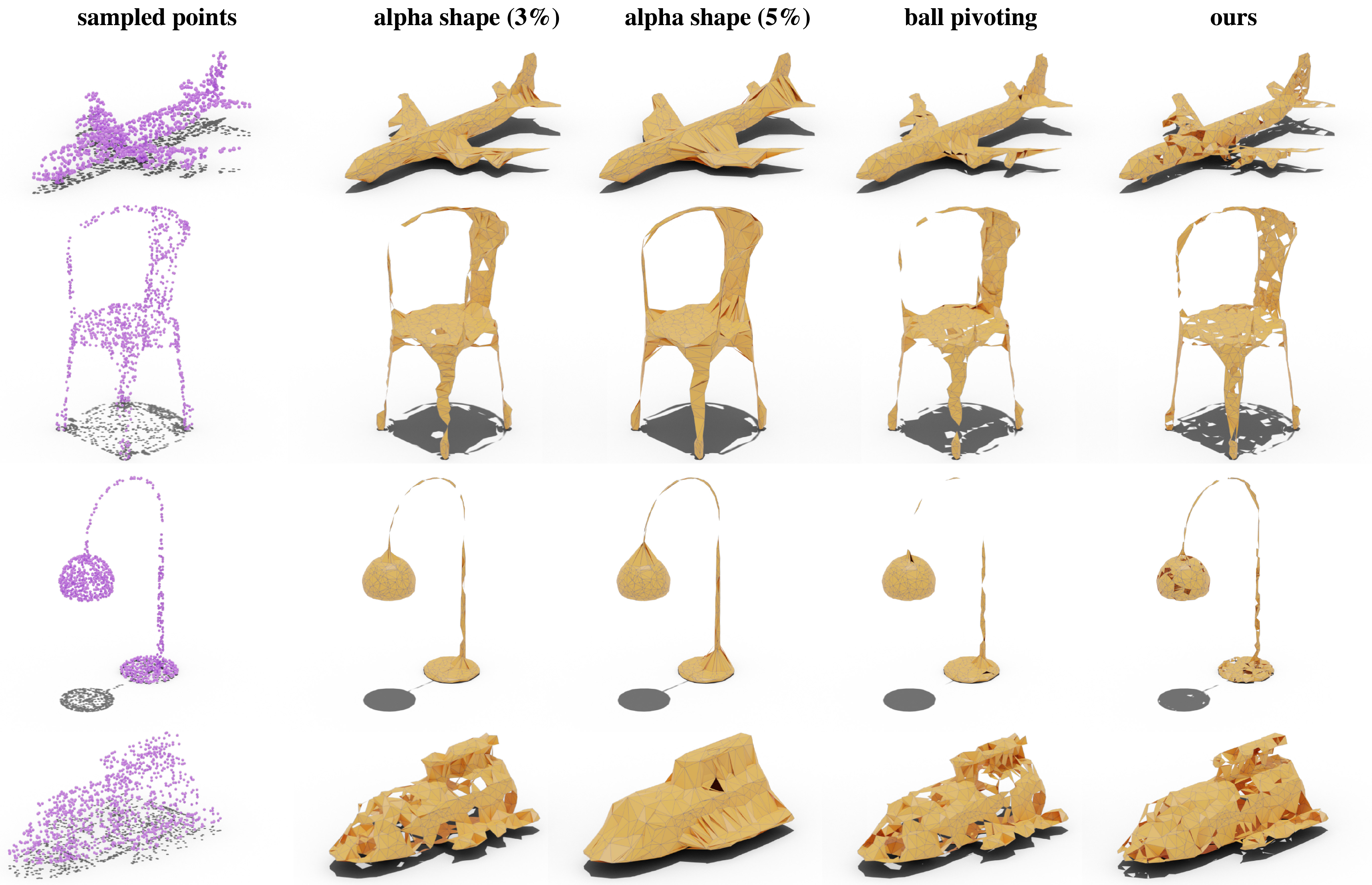
A selection of outputs from PointTriNet and baselines on ShapeNet. The input is 1k points sampled on the surface of the shape, and the output is a mesh using those points as vertices. Constructing point set triangulations which are both accurate and watertight is still an open problem, but our method shows that a differentiable, learning-based approach can yield results competitive with classical computational geometry schemes.

Our method is data-driven, but its geometric nature leads to excellent generalization. Left: reconstructing a synthetic model with vertices of varying regularity and density. Right: reconstructing a 3D range scan of a cathedral. Both use our networks trained on uniformly-sampled ShapeNet.
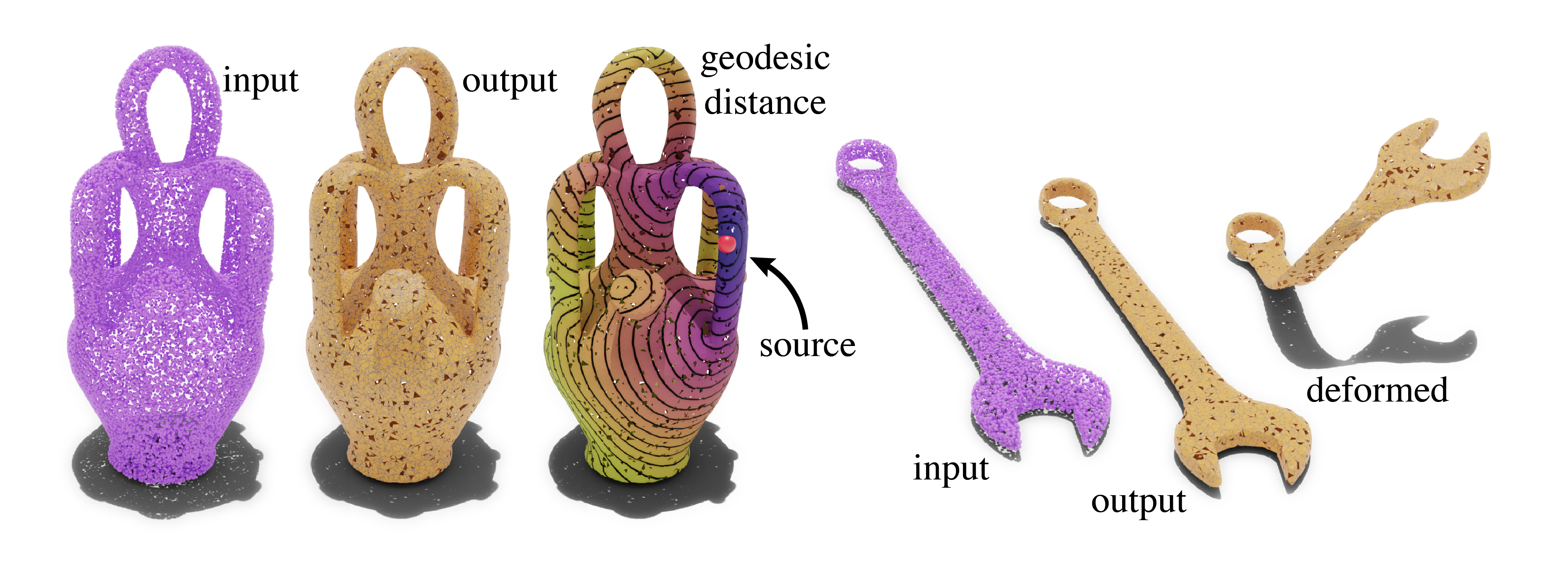
PointTriNet directly generates a triangle mesh, opening the door to many standard geometric algorithms. Left: geodesic distance is computed from a source point. Right: a reconstructed object is deformed via an anchor at one endpoint.
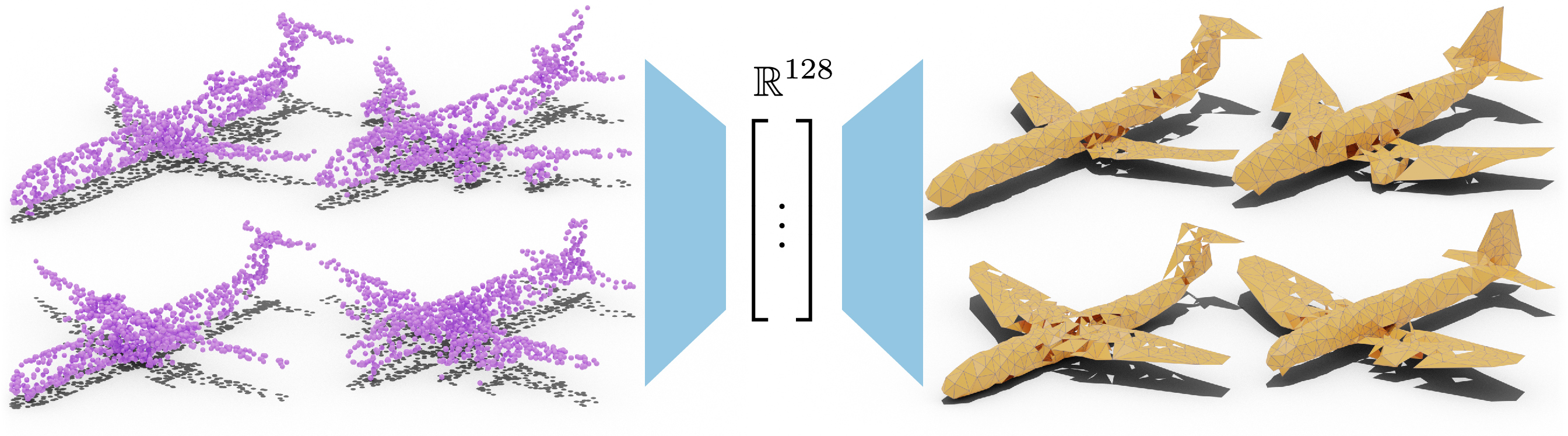
A preliminary example of an autoencoder, which uses our method to directly output a mesh without any intermediate volumetric representations. Input point clouds (left) are decoded to meshes with 512 vertices (right).