I’m a researcher in geometry processing, computer graphics/vision, and 3D machine learning. My work seeks new algorithms and new representations to make computing with geometric data easy, efficient, and reliable. Currently, I’m a Senior Research Scientist at NVIDIA, based out of Seattle, WA.
Previously I received my PhD in Computer Science from Carnegie Mellon University advised by Keenan Crane, and was a postdoc in the University of Toronto DGP with Alec Jacobson. Even earlier, I was an undergraduate at Virginia Tech, where I worked with T.M. Murali on computational systems biology, and was active in competitive programming. Outside of work, I’m a big fan of long-distance running, hockey, and cooking.
NewsResearch
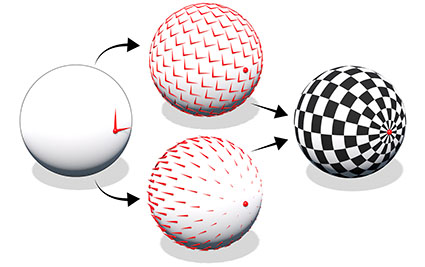
The Affine Heat Method
SGP 2025
The logarithmic map is a local coordinate system about a point, useful in many algorithms. We compute it quickly and robustly via heat flow, by adding a homogenous translation component to the Laplacian.
Uniform Sampling of Surfaces by Casting Rays
SGP 2025
Sampling uniform points on implicit surfaces is hard, but casting rays is easy. We study a classic relationship between the two, sampling points by casting rays—it’s very useful for geometry processing: sampling loss functions, numerical integration, and more.

Stochastic Preconditioning for Neural Field Optimization
SIGGRAPH 2025
A nearly one-line change that improves fitting of neural fields, across many architectures and tasks. The idea is to blur the field during training, evaluated in-expectation by perturbation.
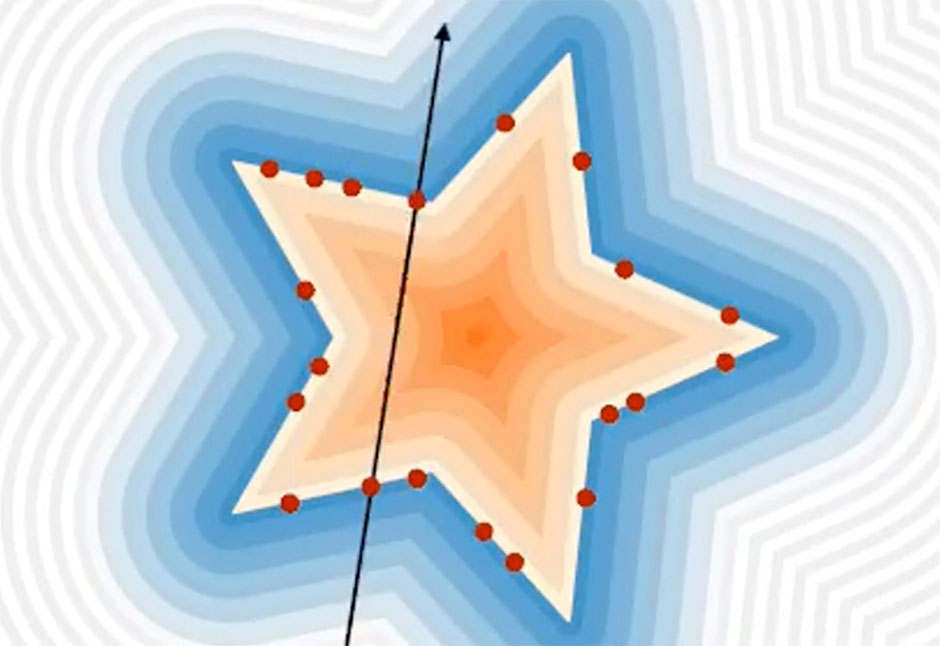
Stochastic Barnes-Hut Approximation for Fast Summation on the GPU
SIGGRAPH 2025
The Barnes-Hut data structure hierarchically accelerates spatial kernel evaluations like electrostatics and winding numbers. Our Monte Carlo approach makes it unbiased, and gives big speedups on the GPU.

Putting Rigid Bodies to Rest
SIGGRAPH 2025
Imagine randomly rolling a rigid 3d object, can you predict what orientations it might land on, and with what odds? We do this via direct geometric analysis, and even show inverse optimization to turn any shape into dice with target probabilities.

Neurally Integrated Finite Elements for Differentiable Elasticity on Evolving Domains
SIGGRAPH 2025
Differentiable elastic simulation for optimization and inverse design of mechanically strong shapes. The key ingredient is a tiny neural network that samples good quadrature points on evolving mesh elements.

SpaceMesh: A Continuous Representation for Learning Manifold Surface Meshes
SIGGRAPH Asia 2024
An embedding space for guaranteed-manifold meshes via the halfedge data structure. Represent polygonal mesh connectivity by a fixed-dimensional real vector at each vertex. Enables high-quality mesh generation in machine learning.

3D Gaussian Ray Tracing: Fast Tracing of Particle Scenes
SIGGRAPH Asia 2024
Fast differentiable ray tracing for particle-based scene representations. High-quality reconstruction from images. Easily support incoherent rays, secondary light effects, non-pinhole cameras, and more.

Surface-Filling Curve Flows via Implicit Medial Axes
SIGGRAPH 2024
Generate smooth space-filling on surfaces via a simple and fast geometric flow. The flow is driven by the medial axis, but we never need to explicitly compute it.

Simplicits: Mesh-Free, Geometry-Agnostic, Elastic Simulation
SIGGRAPH 2024
Automatically fit neural skinning weight fields as a latent reduced representation for efficient deformable simulation of nearly any geometry, including meshes, NeRFs, splats, CT scans, and more.
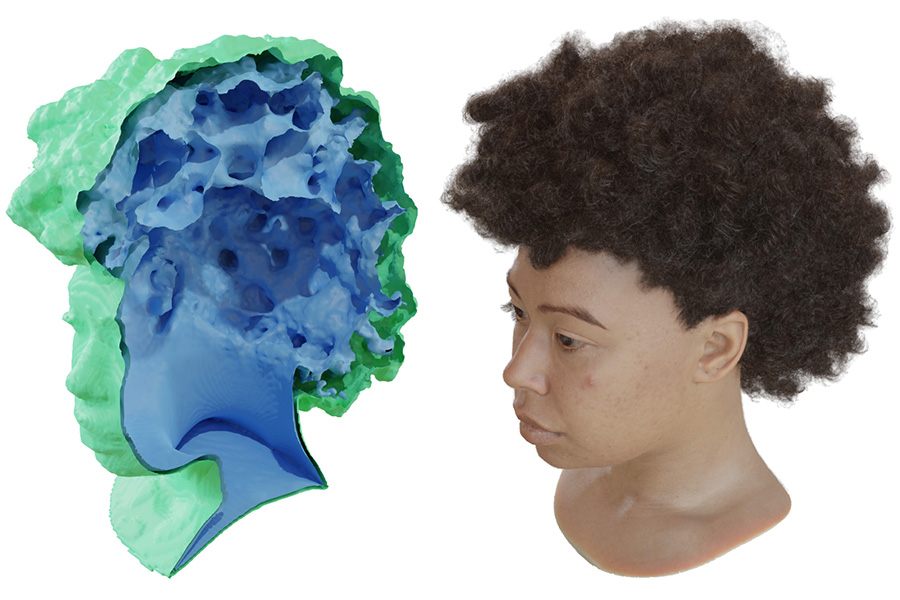
Adaptive Shells for Efficient Neural Radiance Field Rendering
SIGGRAPH Asia 2023 Best Paper Award
Greatly accelerate neural field rendering by extracting bounding shell meshes, and casting rays to sample only that narrow region. Retains volumetric quality, while reducing to fast single sample rendering for hard-surface content.
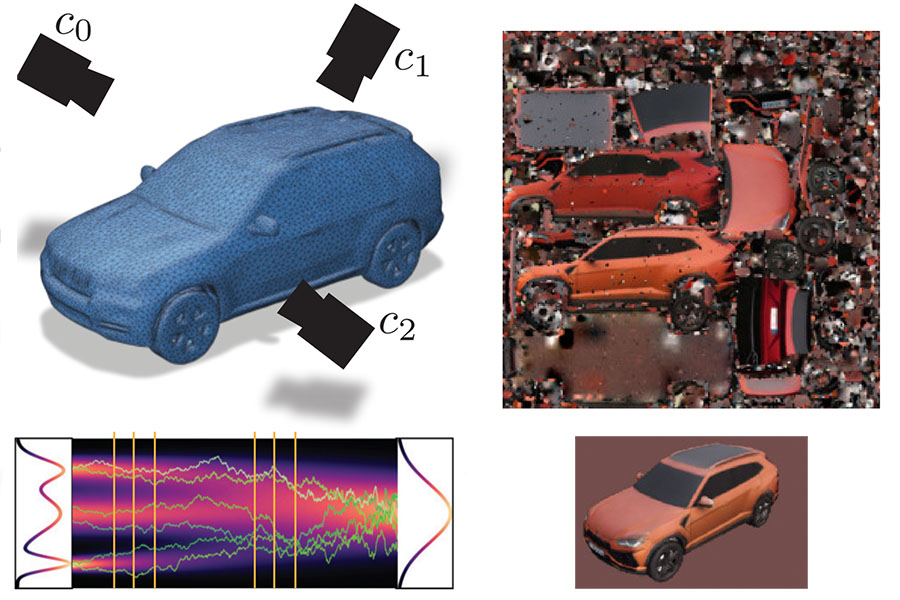
TexFusion: Synthesizing 3D Textures with Text-Guided Image Diffusion Models
ICCV 2023 (Oral)
Synthesize textures 3D geometries by sampling from existing image diffusion models. Rather than using an expensive optization process, we show how to sample the model simultaneously from a set of camera views.

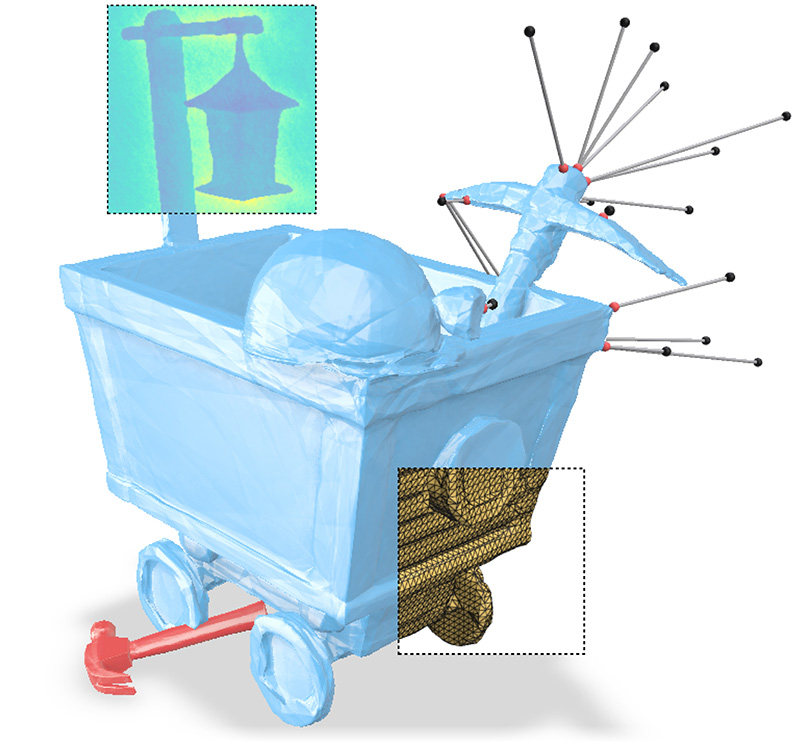
Flexible Isosurface Extraction for Gradient-Based Mesh Optimization
SIGGRAPH 2023
Isosurface mesh extraction, for tasks where you iteratively optimize a surface for some objective. Significantly improves fits & element quality vs marching cubes (etc) by introducing additional DoFs that locally adapt the mesh.
Surface Simplification using Intrinsic Error Metrics
SIGGRAPH 2023
Simplify intrinsic triangulations on surfaces to construct concise hierarchies which respect the intrinsic geometry and are well-suited for geometric computation.

Spelunking the Deep: Guaranteed Queries on General Neural Implicit Surfaces via Range Analysis
SIGGRAPH 2022 Best Paper Award
Efficiently evaluate geometric queries like ray casting, intersection testing, closest-point, and more on existing neural implicit surface architectures. Works on general (not-necessarily-SDF) networks, so it can be used e.g. for occupancy networks or after random initialization.

DiffusionNet: Discretization Agnostic Learning on Surfaces
SIGGRAPH 2022
Simple and scalable deep learning on meshes, points clouds, etc., via spatial diffusion. The networks automatically generalize across different samplings, resolutions, and even representations. Spatial support is automatically optimized as a parameter!
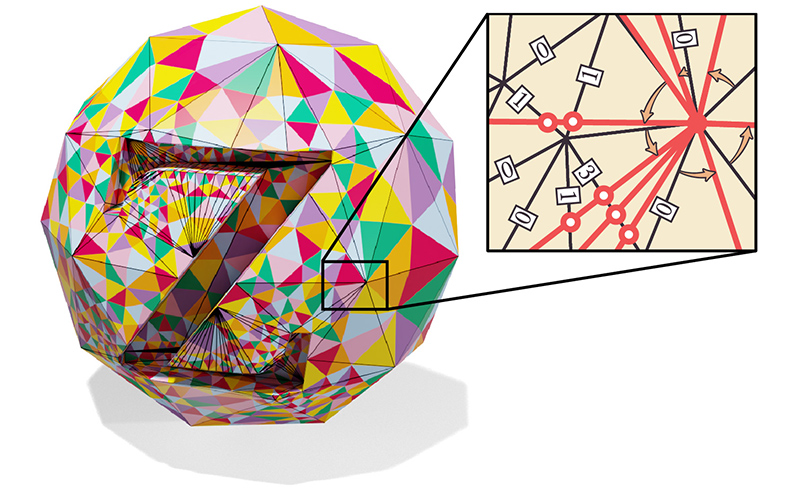
Integer Coordinates for Intrinsic Geometry Processing
SIGGRAPH Asia 2021
Intrinsic triangulations are great for robust mesh processing—now we can represent them via integers, escaping many pitfalls of floating point and offering a strong guarantee of validity while remaining fast and general.
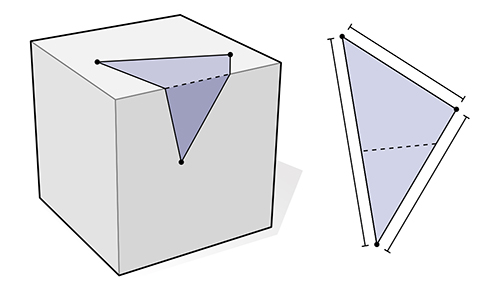
Geometry Processing with Intrinsic Triangulations
SIGGRAPH 2021 Course, IMR 2021 Course
Intrinsic triangulations encode a mesh’s geometry via edge lengths rather than vertex positions, enabling new robust algorithms and much more. This course gives a general overview, covering core theory, implementation, and the latest research.
Intrinsic Triangulations in Geometry Processing
PhD Thesis, Carnegie Mellon University
This thesis treats the theory and practice of intrinsic triangulations, with applications to robust geometric computing. It describes new techniques including representations, retriangulation schemes, flip-based algorithms, and generalizations.
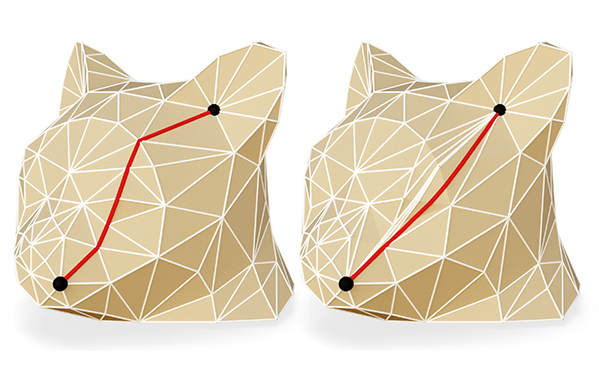
You Can Find Geodesic Paths in Triangle Meshes by Just Flipping Edges
SIGGRAPH Asia 2020
A simple greedy strategy of intrinsic edge flips will provably shorten a given path, loop, or curve network to an exact, locally-shortest geodesic. The procedure also generates a triangulation with these geodesics as edges, which is useful for many applications.

A Laplacian for Nonmanifold Triangle Meshes
SGP 2020 Best Student Paper Award
We extend intrinsic triangulations to apply to any triangle mesh, even those that are nonmanifold and have boundary—the resulting high-quality Laplacian improves the performance and robustness of many algorithms. This strategy also yields a point cloud Laplacian with similar properties!
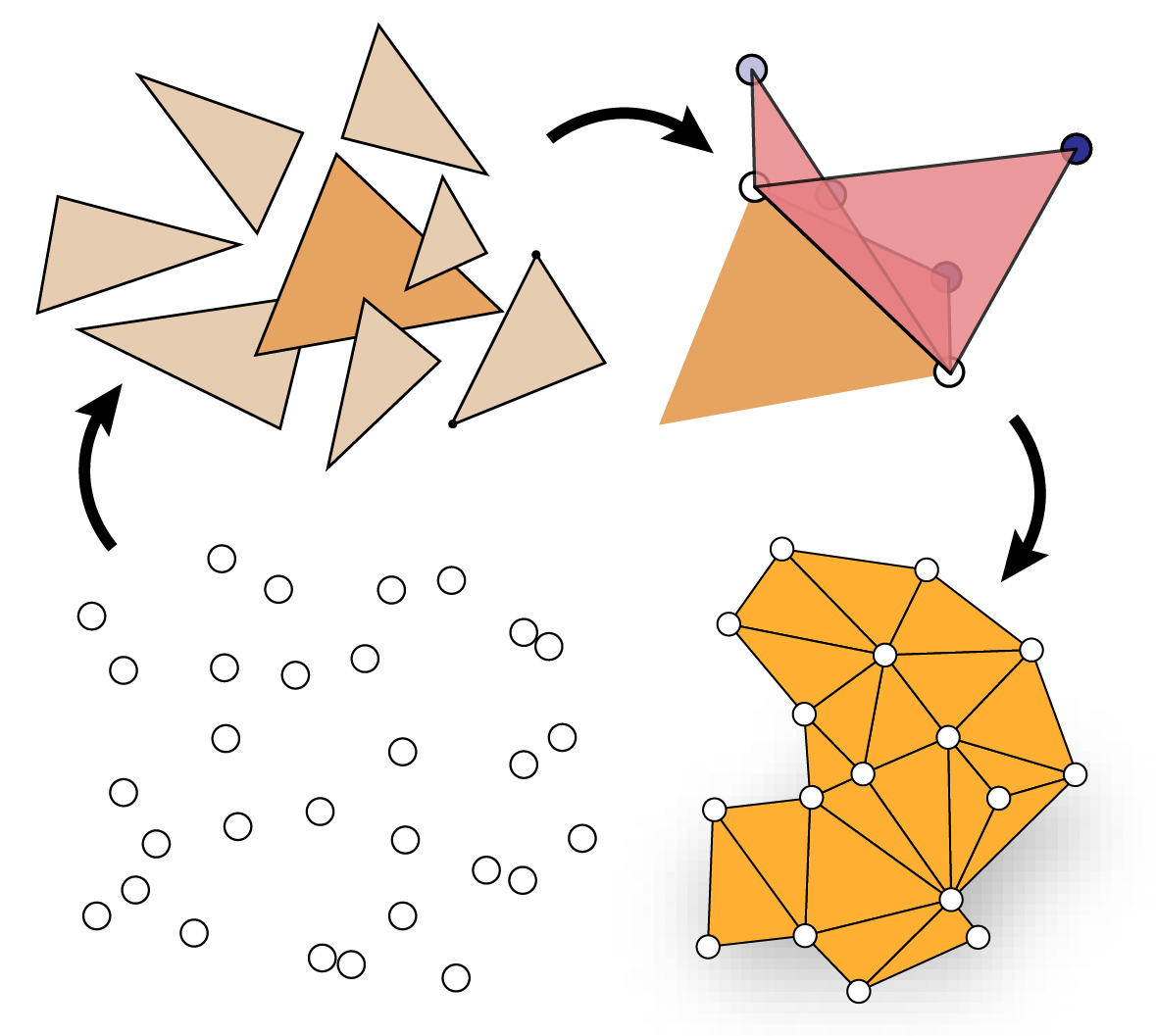
PointTriNet: Learned Triangulation of 3D Point Sets
ECCV 2020
What if we tried deep point set triangulation? PointTriNet presents a classifier + proposal architecture, iteratively generating triangles in a mesh. The method is general, scalable, and differentiable, serving as a triangulation layer for 3D learning.

Navigating Intrinsic Triangulations
SIGGRAPH 2019
We describe a data structure for encoding high-quality intrinsic triangulations on top of a low-quality input mesh. This data structure serves as a black box for robust geometric computation.
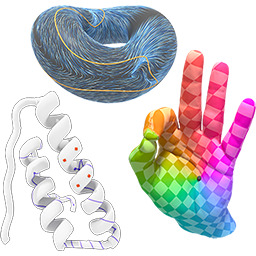
The Vector Heat Method
SIGGRAPH 2019
We show that parallel transport is effectively computed via short-time heat flow. In turn, this leads to efficient algorithms for velocity extension, computing the log map, and much more.

Variational Surface Cutting
SIGGRAPH 2018
Good surface cuts are short, yet allow a shape to be flattened with little distortion. Here, we show shape optimization can be applied to the Yamabe equation to directly compute smooth cuts with arbitrarily low distortion.
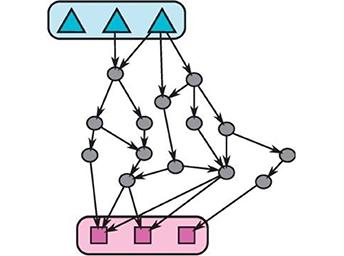
Xtalk: a path-based approach for identifying crosstalk between signaling pathways
Bioinformatics 2016
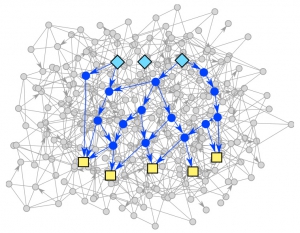
Pathways on demand: automated reconstruction of human signaling networks
npj Systems Biology and Applications 2016
Software
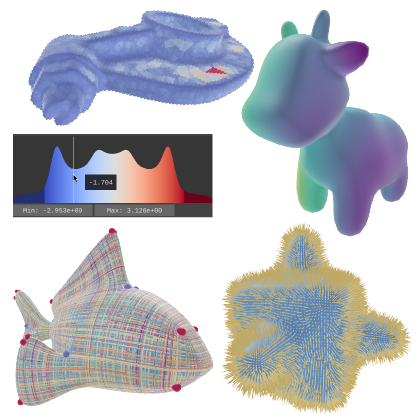
Polyscope
2022 SGP Software Award Winner
A C++ & Python viewer and user interface for the rapid prototyping and debugging of geometric algorithms in 3D geometry processing. The lofty objective of Polyscope is to offer a useful visual interface to your data via a single line of code.


Happly
A C++ header-only parser for the .ply file-format. Includes reading and writing in plaintext or binary mode, general and mesh-specific elements, and automatic type promotion.
